| Definitions | Y, t.2, t.1, 0, +r, e, *, 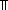 (op,id) lb (op,id) lb  i < ub. E(i), r i < ub. E(i), r +gp, +gp, 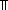 lb lb  i < ub. E(i), < i < ub. E(i), <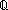 +*>, +*>, 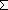 (r) i (r) i  k < j. E(k), k < j. E(k),  a a  j < b. E(j), SQType(T), False, delta(i;j), {T}, suptype(S; T), S j < b. E(j), SQType(T), False, delta(i;j), {T}, suptype(S; T), S  T, P T, P  Q, Q,  A, A c A, A c B, True, B, True,  T, ff, P T, ff, P   Q, P & Q, P Q, P & Q, P    Q, tt, i Q, tt, i  j < k, j < k,   x. t(x), x. t(x),  , {i...}, t , {i...}, t  T, p T, p   q, if b then t else f fi , x(s), {i..j q, if b then t else f fi , x(s), {i..j }, A }, A  B, P B, P   Q, Q,  x:A. B(x), Dec(P), Unit, x:A. B(x), Dec(P), Unit,  , ,  |